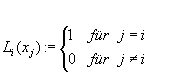
2.3.2 Die Interpolationsformel von Lagrange
Wir benötigen zunächst die Lagrange‘schen Hilfspolynome Li Î Õ n für i = 0, 1, ..., n. Sie sollen so konstruiert werden, dass sie den Wert 1 an der Stützstelle xi annehmen und den Wert 0 an allen anderen Stützstellen xj.
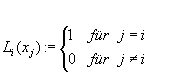
Anscheinend erfüllen folgende Polynome diese Forderung:
![]() =
= 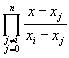 (3)
(3)
Wie wir oben nachgewiesen haben, ist die Lösung für das Interpolationsproblems eindeutig. Daraus folgt , dass auch die Hilfspolynome Li jeweils eindeutig bestimmt sind, das heißt, dass es keine anderen Polynome gibt, die diese Bedingungen erfüllen. Somit können wir die Lösung P des Interpolationsproblems durch die Li‘s konstruieren:
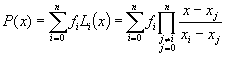 (4)
(4)
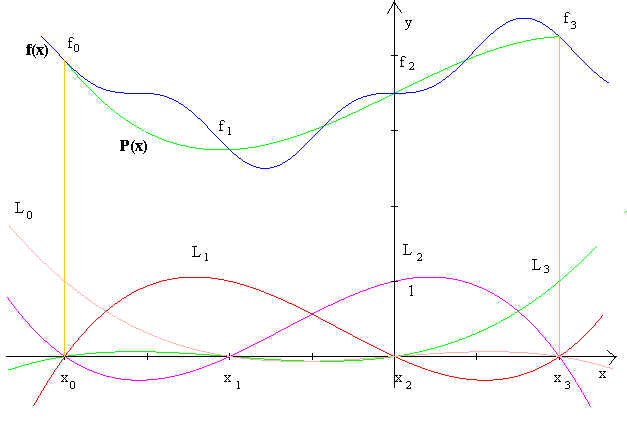
P ist ein Polynom vom Grad n ist, das an den Stützstellen xi die Stützwerte fi annimmt. Daraus ist ersichtlich, dass P linear von den Stützwerten fi abhängt. Die untenstehende Abbildung dient zur Veranschaulichung der Approximation.
Hier wurde die Funktion f(x)=(sinx)3+3.5 (blau) durch ein Polynom dritten Grades P(x) (grün) interpoliert. Folgende Werte wurden durch Computerberechnung ermittelt und werden auf vier Stellen verkürzt ausgegeben.Die Lagrangepolynome Li: L0(x) = -0.0208x3 + 0.0833x
L1(x) = 0.0625x3 + 0.125x2 –0.5x
L2(x) = -0.0625x3 – 0.25x2 +0.25x +1
L3(x) = 0.0208x3 + 0.125x2 + 0.1666x
Die Linearfaktoren fi : f0 = 3.9334
f1 = 2.7481
f2 = 3.5
f3 = 4.2518
Für das interpolierende Polynom ergibt sich daraus:
P3 (x) = -0.0403x3 + 0.537x + 2.5
Dieses Polynom stellt nun die eindeutige Lösung für das gegebene Interpolationsproblem dar.